提要：激光颗粒大小测试的结果与颗粒形状密切相关。通过对椭圆衍射谱的研究, 提出在激光粒度分析中以椭圆谱代替球形颗粒谱。计算机模拟计算与对金刚砂实测的结果表明椭圆衍射模型可以有效地抑制粒度反演结果的展宽, 更准确地获得非球形颗粒群的粒度分布。

关键词　激光衍射, 椭圆模型, 颗粒大小分析, 颗粒形状, 反演

1　引言

由于颗粒大小对粉末材料的重要影响, 颗粒粒度测试在建材、化工、石油等许多领域已经成为一种不可缺少的检测技术。由于颗粒形状的多样性, 无论何种测量方法, 均需要颗粒模型。通常假定颗粒为球体, 与被测颗粒等体积的球体直径称为粒径, 或称等效粒径[1] 。然而球体模型在激光衍射(散射) 粒度分析技术中却遇到严重困难—对非球形颗粒测试常常产生较大误差, 表现为所测得的粒度分布较真实分布有展宽且偏小。来自日本和美国的颗粒测试报告也有相同的倾向[2] 。从光学原理上看，激光粒度分析技术是通过检测颗粒群的衍射谱来反演颗粒群的尺寸分布的。非球形颗粒的衍射谱与球体有很大不同: 前者是非圆对称的, 而后者是圆对称的。欲使二者具有可比性需要新的物理模型, 新的模型应满足: 1) 更加逼近真实颗粒;2)对一系列颗粒有普遍的适用性;3)可给出衍射谱解析式;4)在激光测粒技术中能校正颗粒形状引起的测量误差;5)能函盖球体模型。本文将证明椭圆衍射模型是满足以上条件的最佳选择。

2　非球形颗粒衍射模型的椭圆屏逼近

颗粒虽然是三维物体, 但是在激光测粒技术中其横截面是使光波发生衍射的主要几何因素, 因此只需研究与入射光垂直的颗粒横截面。球体衍射模型即是取颗粒的体积等效球的投影圆作为该颗粒的衍射模型。如图1 所示, 将形状任意颗粒的横截面视为一衍射屏。可分别做出其轮廓的最大内接圆和最小外接圆。设外圆直径为2b, 内圆直径为2a。分别以2a, 2b 为长短轴做椭圆。下面将证明该椭圆屏即为与图1 所示的颗粒横截面等效的非圆屏的最佳解析逼近。

2. 1非圆屏与椭圆屏的几何关系

由图1 可见，与非球颗粒相对应的椭圆屏的面积S e 恰好为其横截面外接圆与内接圆面积的几何中值，而与该椭圆屏面积相等的圆( 面积等效圆) 的直径Do 恰好为其长短轴2a 与2b 的几何中值。

 

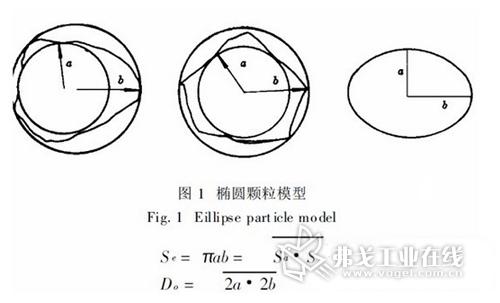
此颗粒对球体的偏离可用形状系数K 表示, K 定义为:

K=b/a

由以上几点可见, 椭圆屏模型的几何要素表明, 它是介于外接圆与内接圆之间的非球颗粒的形状上的最佳解析逼近。

2. 2　非圆屏衍射谱与椭圆屏衍射谱的关系

衍射谱的测量是用典型的二维傅里叶变换光学系统, 如图2( a) 所示。被测颗粒置于平行激光束中, 在傅氏透镜后焦面上即可获得其衍射谱[ 3] 。颗粒衍射谱的探测通常采用同心环状阵列光电探测器进行〔见图2( b) 〕。光电信号经转换后送入计算机作数据处理。

图4示出了与某椭圆屏相关的三支谱线: I a 为内接圆屏强度谱，I b 为外接圆屏强度谱，I e为该椭圆屏的径向谱。据衍射原理可知，轮廓介于如图1所示的内外圆之间的任意形状屏的径向谱必然介于I a 与I b 之间。而由图4 知与该任意形状屏对应的椭圆屏的径向谱I e 恰好位于其间，因此可作为任意形状屏的径向谱的最佳解析逼近。由以上两节的分析可得出如下结论：由同心环状探测器测得的任意形状颗粒的衍射强度谱可用如上定义的与该颗粒相应的椭圆屏的径向强度谱作为其最佳解析逼近。该椭圆屏即为任意形状颗粒的椭圆衍射模型。

3 用椭圆屏模型探讨非球形颗粒衍射谱的展宽机理。

考察一组面积相等而形状系数K不等的椭圆, 其几何参量见表1。图5给出了计算机根据椭圆模型衍射谱解析式(8)绘制的该组椭圆的能谱。所谓能谱即强度谱对各环状探测器面积上的积分值。由于探测器环带面积由内向外是增大的，因而能谱高频部分被放大，更有利于观察其细节差异。

 

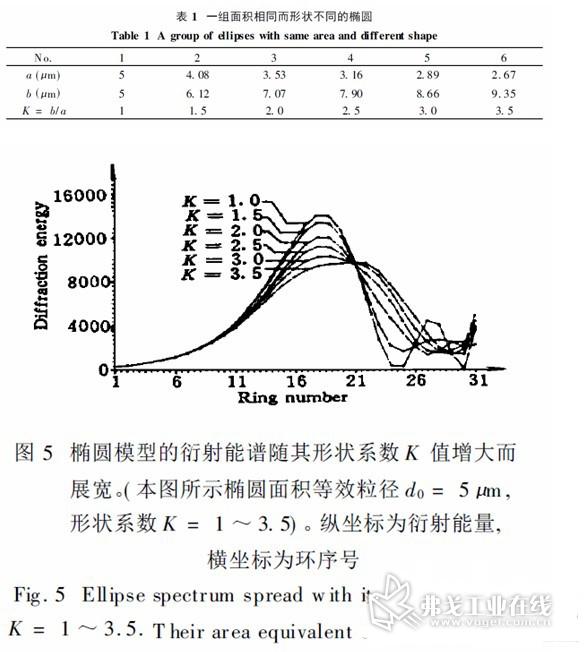
该组椭圆具有相同的面积和等效面积圆直径，但形状不同。据衍射理论知其衍射谱应是不同的。正如图5 所示，使用椭圆模型绘制的能谱图清楚地反映出了这组颗粒的衍射谱间固有的差别。但如果使用球体模型，由于该组颗粒的体积相同，均可用同一个球-圆屏-代表，则不能反映出其衍射谱间的差别。这正是球体颗粒模型的致命缺陷。

图5 表明，形状系数K = 1 时，椭圆模型的衍射谱与球体模型的等效面积圆的衍射谱线相同;当K 值增大时，谱线相应展宽，同时谱线峰值空间频率也相应提高。据(9)式可知，衍射谱分布的展宽必将导致颗粒群粒度分布反演结果的展宽。这正是非球性颗粒在激光粒度分析中产生测量结果展宽的原因所在。

4椭圆模型与球体模型用于粒度反演结果的比较

激光测粒理论认为，忽略相干噪声，颗粒群在各环的衍射能量正比于各级颗粒的衍射谱

在相应单元上，以颗粒组成为权重的线性叠加[5]。用矩阵可表示为：

E = WT

Ei (i = 1， 2，…n) 为颗粒群在第i环的产生的衍射能量。n为探测器有效单元数。

Wj( j = 1，2，…，m) 为直径为D j的颗粒在颗粒群中的重量( 或质量) 百分比，W称为颗粒组成或颗粒分布。m为颗粒分级总数。Tij为第j级颗粒在第i环探测单元产生的衍射能量。T称为标准衍射矩阵。标准衍射矩阵T由m种不同粒径的球体颗粒的衍射谱构成，称为球体标准衍射矩阵。如果矩阵由m种大小不同的椭圆屏衍射谱构成，则称为椭圆标准衍射矩阵，记为T′。据(9)式，如能测得颗粒群的衍射能谱E，即可由计算机根据标准衍射矩阵T 反演颗粒组成W[6]。为了比较不同的颗粒模型对同一颗粒群粒度反演结果的影响，现仅以K = 2的某颗粒群为例, 给定其颗粒组成W0( 见表1) 。用相应的椭圆屏群的衍射能谱E 作为(9)式中的测得能谱。分别使用球体标准衍射矩阵T 和椭圆标准衍射矩阵T′对E进行反演运算, 结果列于表2。

粒度分布曲线示于图6

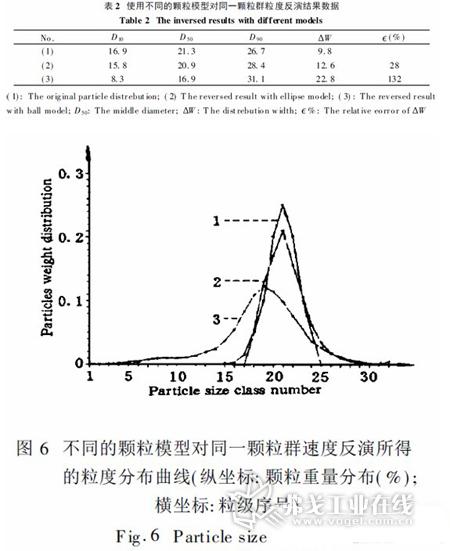
从反演结果可以看出, 球体模型用于非球形颗粒群的粒度反演必将导至粒度分布的展宽和中位径偏小。本例中( 3) , W 的宽度扩大了132% ; 中位径偏离了4. 4 m,使用椭圆模型, 则可以得到相当好的分析的结果。本例中(2) D50与预先设定值的偏差只有0. 4 m, 宽度误差为2. 8 um, 是设定宽度的28%。此误差来自反演过程截断误差的积累。与前者相比误差压缩了1. 04倍。

图6 中(1)为该颗粒群的固有组成;(2)为采用椭圆模型拟合的结果; (3)为采用球体模型拟合结果。从图中可清楚看到曲线(2)更接近曲线(1) , 而曲线(3)则比曲线(1)明显地展宽了。由此可见椭圆模型用于激光粒度分析可以大大提高测量结果的准确度。为了说明椭圆模型的应用效果, 表3 给出了两种颗粒模型对4种金刚砂磨料微粉衍射数据的拟合结果与显微镜测量结果的比较。根据金刚砂形状特征椭圆模型的形状系数取K = 2。

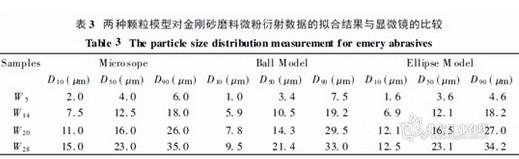
显微镜测粒度是一种直接测量法, 以它为基准考察球体模型与椭圆模型的反演结果是合理的。比较表3 中几种磨料的中位径D50及分布宽度W = D90 - D10,可以发现,椭圆模型的反演结果比球体模型更接近显微镜的测量结果,有更高的拟合精度。可以认为,椭圆模型是一种在非球形颗粒激光测试中广泛适用的颗粒模型。

5　结　论

本文提出在激光粒度分析中用椭圆颗粒模型代替球体模型,它比球体模型更加逼近非球形颗粒。椭圆衍射谱可以作为一类颗粒衍射谱线的代表, 此类颗粒的外接圆与内接圆直径分别与该椭圆的长、短轴长度相同。研究结果表明,非球形颗粒衍射谱比其等效体积球的衍射谱有所展宽, 展宽的程度与其形状系数有关。

采用适当的椭圆屏衍射谱构造的标准衍射矩阵能有效地抑制反演结果的展宽等误差。本项研究将颗粒形状与颗粒大小测量相联系, 提出了椭圆衍射模型。此模型对提高激光粒度分析的精度、扩展其使用领域具有重要的实用价值。